Figura

Ognuno di noi comunica visivamente in ogni momento della giornata e della vita, da sveglio e da addormentato (anche le posture del sonno rivelano …).

Il portamento e il comportamento sono caratterizzati, infatti, da figure. Tali figure possono essere analizzate, riprese, riprodotte, raffigurate, rappresentate, codificate. Le figure costituiscono la grammatica tridimensionale visiva del sentimento, dell’emozione e del discorso prodotti dall’individuo nella sua relazione con lo spazio, la società, gli eventi! Queste figure ci esprimono. Dicono tutto di noi. Attenti alle figure, quindi!

Il portamento, cioè il modo di camminare, di muoversi e di atteggiarsi di una persona, può fargli fare una bella o una brutta figura; ognuno ha, infatti, uno stile (inconfondibile segnale di appartenenza all’ambiente, alla cultura, al  sociale, alle convenzioni …). La moda ha il suo fascino, proprio in quanto si nutre di stile, più che produrne!

Il comportamento, cioè l’azione e la reazione che un organismo manifesta in  risposta ad uno stimolo proveniente dall’ambiente esterno, segnala, ancor più del portamento, l’educazione: l’effetto degli insegnamenti e delle esperienze personali, accumulatisi nel tempo, si rende evidente nel momento preciso, in cui bisogna reagire ad un evento inatteso, ad una situazione difficile, ad una scelta obbligata, rivelando caratteri …

Anche in questo caso è una questione di stile: c’è chi tace, chi sospira, chi bestemmia, chi fisicizza …!

Diventiamo tutti dei figuranti, e, come tali, oggetto di raffigurazione! Unici animali, tuttavia, ad essere nello stesso tempo oggetti e soggetti … figurativi.

Ogni sport possiede figure tipicizzanti. Ogni atleta è noto e diventa famoso e caro ai suoi tifosi soprattutto per le sue figure stilistiche, piuttosto che per le … figure fatte (per esempio, Maradona per il suo inconfondibile passo, Tomba per la reattività in curva, non certo per stili di vita …). Inconfondibili stili. L’atleta, che possiede il suo stile, lo riconosci immediatamente alla distanza.

Ogni ballo, per quanto libero, produce figure, e gli stessi ballerini, al di là - o forse proprio per ciò – dell’erotismo dei movimenti, godono insieme e competitivamente delle figure che insieme intrecciano nella sala da ballo.

In gara, bisogna dimostrare che si conoscono e s’interpretano bene le figure caratterizzanti quel ballo specifico. Insomma, un tango è un tango è un tango! 

Nessun artista, per quanto bravo, riuscirà mai, sull’immobile superficie del dipinto a riprodurre le figure: esse sono bidimensionalmente in-raffigurabili, esse sono temporalmente in-arrestabili! Occorrono tecniche riproduttive dinamiche, il cinema, la televisione. Tutti i tentativi di fermare il movimento hanno prodotto straordinarie invenzioni formali (dal primo cavallo in corsa dipinto in una grotta paleolitica ai nudi che salgono o che discendono le scale, alle signore che passeggiano con cagnolino al guinzaglio …), che nulla hanno a che fare con il movimento. La loro cattura pittorica è figurativa, ma non effettivamente raffigurativa!

Eadweard Muybridge (1830-1904) Animal Locomotion (Locomozione animale. Uomo che sale le scale, part.), 1887.

Marcel Duchamp, Nu descendant un escalier, n. 2, 1912.

Giacomo Balla, Dinamismo di un cane al guinzaglio, 1912.

Cosa significa, alla fine, il termine figura, per poter passare all’arte che ne fa … soggetto stilistico? Arte, per l’appunto, detta figurativa!

Figura è un termine che deriva dal latino fingere; fingere, ovvero “plasmare con le mani”; esso indicava precisamente il lavoro artigianale e artistico con il quale, utilizzando la creta, si realizzavano, per esempio, le sculture.

Immediatamente ci viene in mente l’azione del ceramista: la semplice arte del costruire vasi contiene al suo interno un liquore filosofico! La povera argilla, materia di bibliche genesi …, che può assumere plastiche forme, e dunque infinitamente (quasi) modellabile, è, proprio per ciò, metafora dell’atto maieutico del filosofo, il quale, come Socrate insegna, non può far a meno di modellare i suoi allievi, anche a scapito della sua vita! Platone, raccontando della condanna a morte del maestro, proprio questo problema pone, nell’Apologia: come è possibile che tutti gli accusatori di Socrate siano buoni educatori e solo lui il corruttore?

Quale la differenza tra insegnamento e plagio? La lezione maieutica raccolta da Platone è immortale: chi sa deve sapere innanzitutto di non sapere e ciò che trasmette ai suoi allievi non può che riflettere questa malinconica condizione, e seminare dubbi ed interrogativi piuttosto che certezze immutabili.

Ciò teme il potere: che si sollevino i problemi e che si modellino teste pensanti. Teste come contenitori, vasi di sapere!

Conclusione, per capire perché siamo partiti con il parlare dell’argilla: lavorare sulla ceramica è lavorare sulla testa, impresa da filosofi! Ma, infatti, per chi non lo sapesse …: “testa” in antico latino significa “vaso d’argilla”, e ancor oggi a Napoli testa sta per “vaso da fiori”! Un’immagine indimenticabile della fragilità dei contenitori … e della bellezza effimera dei pensieri. elf, Mimnermo, Come le foglie in un vaso corinzio, 1990

Il significato etimologico del verbo latino ci fa comprendere come l’immagine fosse originariamente intesa come qualcosa che riproduce fedelmente la realtà, quasi che essa ne sia una sorta di calco.

Il significato attuale del verbo “fingere” nel senso di “voler far credere una cosa diversamente da come essa è” nasce per l’appunto dal fatto che la scultura, in origine, cercando di imitare realisticamente le fattezze del corpo umano, fingeva la realtà!

La parola italiana figura sta dunque innanzitutto a significare la forma o, per meglio dire, l’aspetto esterno di qualcosa, e quindi il modo in cui essa ci “appare”: la pittura e la scultura sono definite, infatti, arti figurative proprio perché sembrano rappresentare l’apparenza reale delle cose.

Il modo in cui la figura ci appare, dunque, è in quanto essa si definisce sul suo sfondo! Una figura è visibile solo per contrasto con ciò che la circonda, con ciò rispetto a cui essa si staglia inconfondibilmente. La figura ha bordi!

Straordinaria natura della figura: essa è concettuale e grafica, mentale e in disegno.

E tuttavia: se pensiamo che l’immagine possa rappresentare la realtà, possiamo essere portati a scambiare l’una con l’altra.

Quando guardiamo una fotografia, o seguiamo un evento, ripreso dalla televisione – lo stesso meccanismo filmico fa leva sul fatto che partecipiamo a ciò a cui stiamo assistendo: altrimenti perché proviamo sentimenti? -, siamo automaticamente portati a credere che ciò che vediamo sia  “vero” o corrispondente al vero.

Tra queste due accezioni c’è tuttavia un abisso: pensare che un’immagine sia vera è ben diverso dal ritenere che essa sia simile al vero. Ovviamente! Anche il più stupido di noi, oseremmo dire, capisce che bella differenza intercorra tra la foto della persona amata e il suo corpo!

Un’immagine vera deve essere certificata dal documento: solo la prova, per così dire, esterna all’immagine, può garantirne la veridicità. Esempio: un taglio particolare dell’immagine, esclude dalla ripresa un elemento che determina il significato complessivo e determinante dell’evento. Un personaggio sta sparando ad un altro, ed è ciò che vediamo! Ma può capitare che, dietro allo sparatore, ci siano un regista, una troupe, una cinepresa e … un fotografo di scena!

La comunicazione visiva dell’immagine, dunque, dipende totalmente dalle informazioni esterne alla cornice, esterne al frame!

Quando, dunque, diciamo che un’immagine è vera, non c’accorgiamo di dire contemporaneamente una cosa giusta e una errata. L’immagine che abbiamo davanti, riprodotta, e in qualche modo rappresentata, è vera!  Ciò di cui possiamo dubitare è l’immagine, o, per meglio dire, la “figura” contenuta nell’immagine!

Il concetto di figura appartiene al rizoma di immagine, ma apre anche un’altra serie di relazioni con i concetti di forma e di configurazione. A legare insieme queste due direzioni di sviluppo è la misura: tant’è vero che, da un punto di vista delle forme e delle configurazioni, la figura si fa …  geometrica (la prima figura geometrica, come tutti ricordiamo, è il punto!).

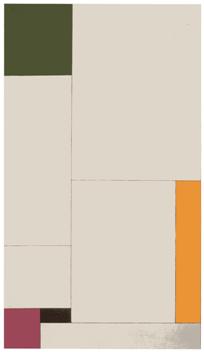Vantongerloo, Composizione derivata dall’equazione y=ax²+bx+18 con verde, arancio, viola (nero), 1930, Salomon R. Guggenheim Museum , New York.

Quando vediamo un numero, prima ancora di pensarlo come calcolo, vediamo insieme una forma (grafica), ma soprattutto cogliamo la sua configurazione concettuale: è come se ci fosse una figura-del-tre, una figura-del-quattro, ecc.

Una figura nella logica è una figura logica. Quali figure riusciamo a ricordare che hanno a che fare con la logica e la misura, prendendo configurazioni?

Innanzitutto le varie serie numeriche son famiglie che son figure, dette insiemi: l’insieme dei numeri naturali, interi, pari, dispari, primi, perfetti, frazionari, decimali, periodici, razionali, irrazionali, reali, complessi, algebrici, trascendenti, transfiniti di Cantor …

Numeri son ritmi! Anima del reale! Per quanto astratti. Per quanto invisibili!

Finchè non appaiono come figure figurate. Come effetti. Non come cause.

Funzioni son figure, proporzioni, equazioni, calcoli …

Le figure dei numeri: così come esistono quelle retoriche del linguaggio[1] vi son quelle ordinative del numero, del ritmo, della configurazione che si dà il pensiero per organizzare in mappe la complessità.

Figure dell’ordine, che il pensiero disperatamente vuol segnare per darsi percorso: reti, rizomi, nodi, frattali, labirinti, diagrammi, schemi, alberi, grafi, grafici, tabelle, stringhe, alfabeti, ideogrammi …

E figure tracciate da macchine che rilevano e rivelano moti vitali (!): sismografie, elettroencelografie, ecografie …

Artisti vari hanno ben capito questo segreto, approfittandone formalmente: Vantongerloo (con le sue equazioni plastiche), Opalka (con le sue numerazioni infinite), Mario Merz (con l’applicazione della legge accrescitiva detta di Fibonacci) …

Ma, in effetti, tutta l’arte si misura con il numero e la figura, soprattutto se non figurativa!

     Ogni rappresentazione del numero equivale ad una rappresentazione del tempo. L’artista Roman Opalka ha iniziato a dipingere il tempo a partire dal 1965, iniziando dall’uno. La numerazione proseguirà opera dopo opera, incessante, indomabile, realizzata rigorosamente a mano. Sempre uguale concettualmente, sempre diversa formalmente. Il nome di quest’opera continua è Opalka 1965/1-oo. Metà della vita di Opalka è trascorsa ripetendo costantemente quest’azione, che si concluderà solo con la morte.

La vastità della produzione artistica di Mario Merz non può, ovviamente, essere sintetizzata unicamente dalla serie cosiddetta di Fibonacci, a cui comunque l’artista è particolarmente legato, e di cui presentiamo qui un’opera significativa.

Dalla testa di un animale imbalsamato si diparte a spirale una serie di numeri successivi, il cui intervallo tra l’uno e l’altro è determinato dall’applicazione d’una formula matematica, la cui invenzione risale al più grande matematico europeo del Medioevo, Leonardo da Pisa, o Leonardo Pisano, nato intorno al 1175 (lui stesso si faceva chiamare Fibonacci, per dire “figlio di Bonacci”).

Fibonacci s’era posto il seguente problema: se un paio di conigli sono collocati in un campo e se essi, diventati fertili dopo un mese, producono un nuovo paio di conigli, quante paia di animali ci saranno dopo dodici mesi?

La formula per calcolare la somma finale deve tener conto della seguente sequenza: 1, 1, 2, 3, 5, 8, 13, 21, ...Ogni nuovo numero è la somma dei due precedenti!

Facciamo vedere due tipi di “figure”, detti schemi, che ci permetteranno di capir meglio il ragionamento.

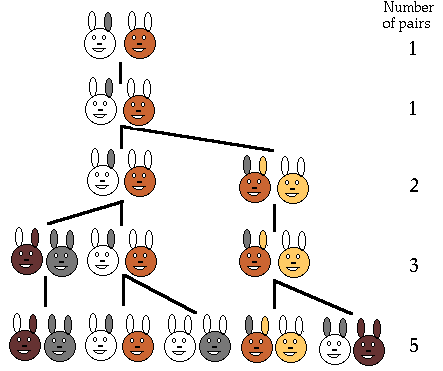
Un altro tipo di figura, o schema, più analitico:

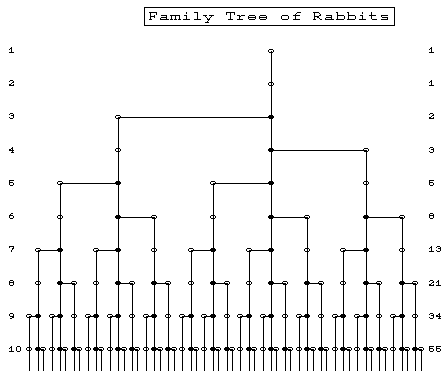
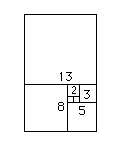
Ma la scoperta di Fibonacci non si limita a questa già importantissima formula; egli scopre che, se dividiamo ogni numero per il suo precedente, otteniamo un numero straordinario:

¹/₁ = 1,   ²/₁ = 2,   ³/₂ = 1·5,   ⁵/₃ = 1·666...,   ⁸/₅ = 1·6,   ¹³/₈ = 1·625,   ²¹/₁₃ = 1·61538...

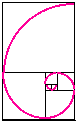
Il numero trovato, 1·618034, è chiamato sezione aurea o numero aureo. O pi greco!

         Gli studi di Fibonacci hanno unìimportanza enorme anche per comprendere alcuni segreti della costituzione profonda della realtà naturale, quella parte invisibile che la scienza non può non portare, prima o poi, nel dominio del visibile.

Queste semplici figure ci permettono di comprendere come sia organizzata ogni forma esistente che si sviluppi a spirale - come la distribuzione dei semi di un girasole o di una pigna o come certe particolari conchiglie (Nautilus, Telescoptum) -.

Il segreto della spirale (spirale logaritmica o equiangolare), che si può prolungare all’infinito, è svelato, infatti, dal nostro primo schema, in cui appare la costruzione geometrica della successione dei rettangoli che la determinano (ogni nuovo rettangolo ha un lato lungo quanto la somma dei lati di due rettangoli precedenti).

Queste ed altre informazioni scientifiche sugli studi di Fibonacci possono essere reperiti in uno dei siti scientifici più belli della rete:

http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html

Quale è, dunque, il significato delle opere di Mario Merz, ispirate alla formula di Fibonacci? Il merito dell’artista, oltre, naturalmente, a quello, implicito, della bellezza del risultato estetico (offerto dalle soluzioni formali, installative e spaziali adottate), consiste proprio nell’aver prodotto una figura concettuale, che ci permette di costruirci un modello mentale dello straordinario ordine costruttivo presente in natura. Un ordine, che l’artista traduce in emozione e in perturbamento. Il numero diventa forma attraverso la … figura!

Ogni sport contiene figure, più o meno acrobatiche. Ogni numero acrobatico produce figure, agli anelli, al trapezio, sul filo sospeso ... Volteggiano circensi sopra le nostre teste, i passi del cavallo nell’arena son figure, gli aerei in gara disegnano looping, tonneau, scampanate, otto, Fieseler …

Per finire danzando: ogni passo di danza, per quanto libera …, è sempre codificato o codificabile. Ogni gioco, infatti, è possibile solo in quanto possiede regole!

Tra tutte le danze scegliamo quella che maggiormente si presta alle coreografie del corpo desiderante: il tango.